(Xuanyue Shentu, Xiaoping Lai, Tianlei Wang, Jiuwen Cao*, Efficient ADMM-Based Algorithm for Regularized Minimax Approximation, IEEE Signal Processing Letters, 2023, published online)
极小化极大(Minimax)逼近法在大规模问题的求解中有着广泛的应用,特别是在信号处理和机器学习领域。用于求解Minimax逼近问题的算法中,对于一维数据有成熟的交错点组方法,但是随着维数的增加,计算复杂度急速增加,对于二维数据缺乏有效的算法。由此,我院人机混合智能与智慧健康研究中心在数字滤波器设计方向的研究论文Efficient ADMM-Based Algorithm for Regularized Minimax Approximation被IEEE信号处理通讯期刊IEEE Signal Processing Letters录用。
交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)非常适合解决各种大规模数据问题。本研究考虑Minimax逼近问题的最优解不是唯一的,通过在代价函数中加入正则化项解决这一问题。然后,本研究在ADMM算法的基础上,提出了一种有效的正则化极小化极大(Regularized Minimax,RMM)逼近问题的标量算法。最后,将这基于ADMM的算法应用于二维有限脉冲响应数字滤波器的Minimax设计和随机神经网络的训练中。实验结果表明,该算法收敛速度快,计算复杂度低,学习逼近模型具有良好的逼近/预测性能。
论文第一作者为2021级硕士研究生申屠轩悦,论文指导老师为赖晓平教授,通讯作者为曹九稳教授,研究获得了浙江省自然科学基金重点项目的资助。
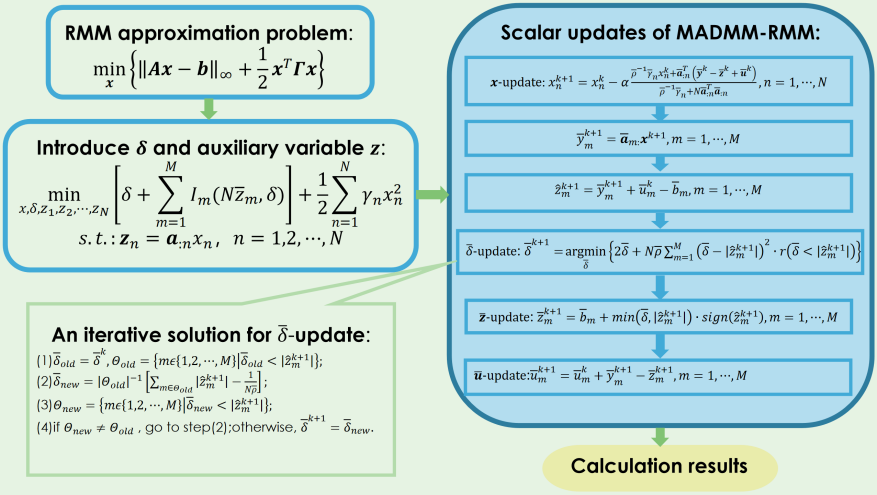
算法核心流程图: