(Xiaoping Lai, Jiuwen Cao, and Zhiping Lin, “An Accelerated Maximally Split ADMM for a Class of Generalized Ridge Regression,” IEEE Transactions on Neural Networks and Learning Systems, 2021, published online, doi: 10.1109/TNNLS.2021.3104840.)
计算负担过重是当今大数据时代机器学习的一个人主要挑战。针对该挑战,近年来我院人机混合智能与智慧健康研究中心在机器学习的并行快速算法方面开展了深入研究。继2020年在IEEE TNNLS发表基于最大分划ADMM的高度并行超限学习机算法之后,今年再次在该期刊发表题为“An Accelerated Maximally Split ADMM for a Class of Generalized Ridge Regression”的长文。该文针对一类广义岭回归问题,提出一个新的可标量化最大分划ADMM算法和一个新的ADMM加速技术,并建立了该加速最大分划ADMM算法的线性收敛性和收敛率,给出了算法参数的选择方案。在GPU平台上的并行实现,以及在面向回归和分类的神经网络训练中的应用,表明该算法比现有算法具有更快的收敛速率、更少的计算时间和更大的GPU加速比。
岭回归(即l2-正则最小二乘)是机器学习领域普遍采用的学习准则,通过增加回归系数向量2-范数的惩罚项限制回归系数的大小,以克服最小二乘回归的过拟合问题。普通的岭回归,对不同的回归系数采用相同的惩罚因子(正则化因子)。不少应用问题,如容错神经网络的训练,需对不同的回归系数施加不同程度的惩罚,以克服回归系数和结点噪声的影响。该论文考虑的广义岭回归问题,就是这样的一个岭回归的扩展。
交替方向乘子法(ADMM)是大规模并行优化的强有力工具,其核心思想是将一个相对复杂和规模较大的优化问题,分解为若干相对简单和规模较小的可并行优化子问题。研究中心率先采用最大分划思想,即将优化模型按优化变量分划为一系列标量优化问题,得到的最大分划ADMM具有高度的并行性和典型的标量化特征,特别适合在众核GPU计算平台上实现。
论文提出一种新的ADMM加速技术,与提出的最大分划ADMM结合,得到一个加速最大分划ADMM算法。采用线性系统稳定性理论和矩阵谱分析,建立了简洁的算法收敛充要条件和线性收敛率。特别需要指出,基于此收敛性分析结果,得到了某特定正则化方案下的最优算法参数,文献中很少见到这样的结果。根据此最优算法参数,论文还给出了实用的算法参数选择方案,为算法的实际应用铺平了道路。
论文作者为研究中心的赖晓平教授、曹九稳教授和新加坡南洋理工大学的林芝平教授。研究获国家自然科学基金重点项目、科技部重点研发计划项目和之江实验室开放课题的资助。
广义岭回归问题:
![]()
加速最大分划ADMM(A-MS-ADMM)算法:
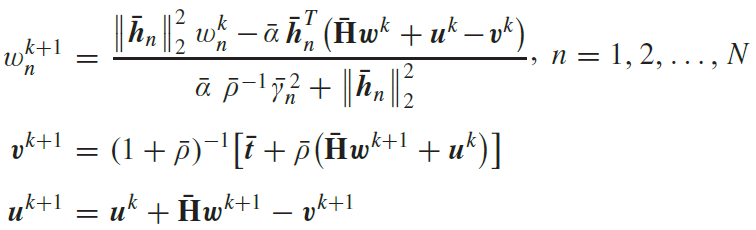
![]()
收敛性能:
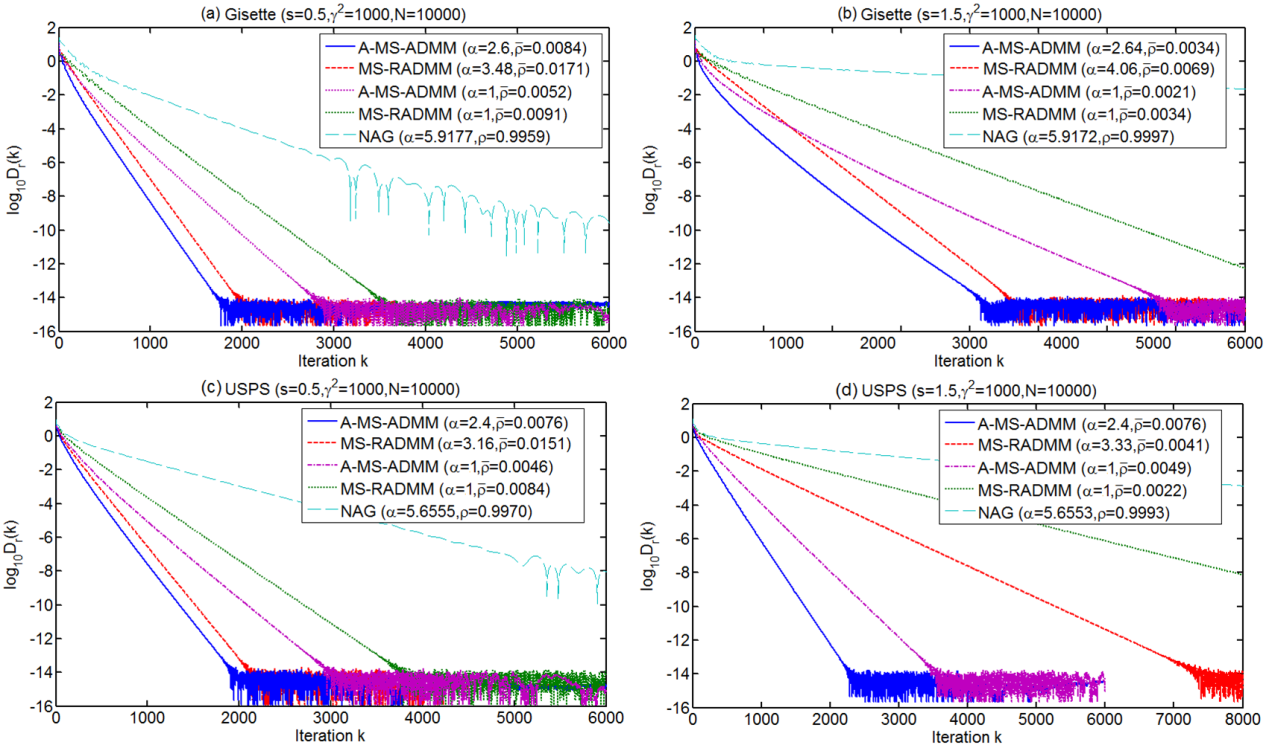
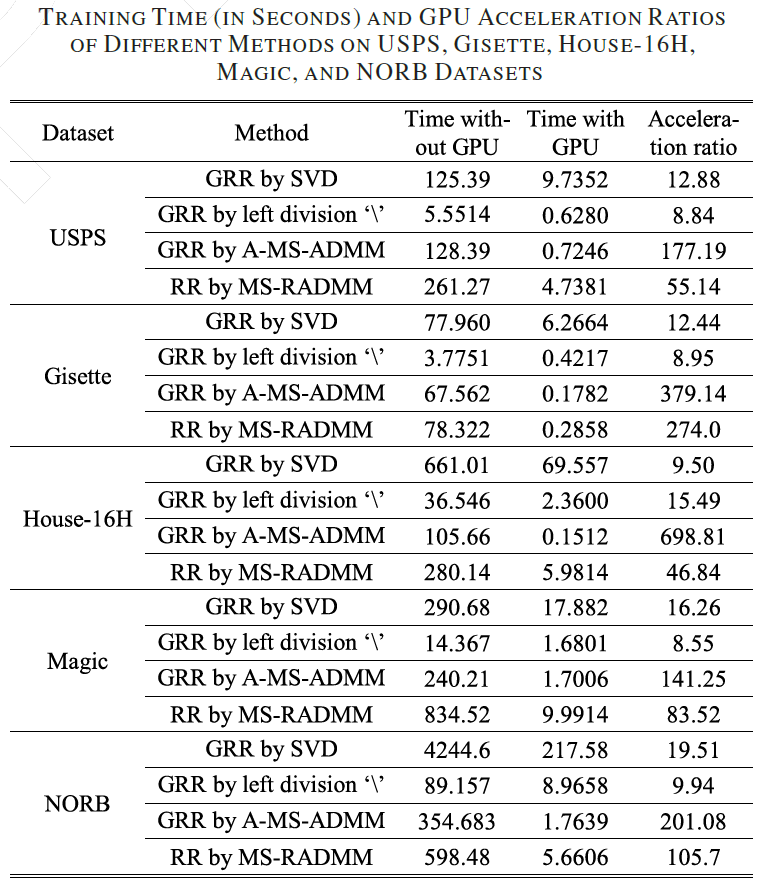
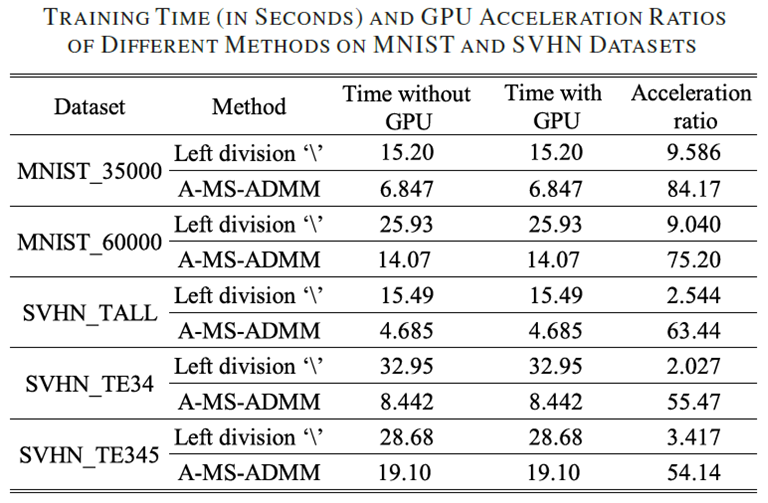
计算时间和GPU加速比: